Sommaire.

Les triangles

Le triangle est un polygone à 3 côtés.

1. Définition
   • Triangle quelconque : triangle n'ayant pas de particularités définie. Ce triangle peut être banal, rectangle, isocèle, équilatéral...
   • Triangle isocèle : triangle ayant 2 côtés de même longueur. Un triangle isocèle peut éventuellement être soit rectangle, soit équilatéral.
   • Triangle rectangle : triangle ayant un angle droit. Un triangle rectangle peut éventuellement être isocèle (en effet, la somme des côtés des 3 triangles faisant 180 ° - voir plus bas - l'un d'eux peux faire 90 ° et chacun des 2 autres, 45 °)
   • Triangle équilatéral : triangle ayant ses 3 côtés de même longueur.
   • Hauteur d'un triangle : il s'agit d'une droite perpendiculaire à un côté du triangle et passant par le sommet opposé. Un triangle a 3 hauteurs.
   • Médiane d'un triangle : il s'agit d'une droite sécante au milieu d'un côté du triangle et passant par le sommet opposé. Les 3 médianes d'un triangle se coupent au point G, centre de gravité du triangle. Un triangle a 3 médianes.
   • Médiatrice d'un triangle : il s'agit d'une droite perpendiculaire au milieu d'un côté du triangle. Un triangle a 3 médiatrices.
2. Propriétés
   1. La somme des 3 angles d'un triangle fait 180 ° (PI rad)

      Démonstration.
      

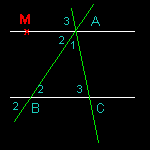
      Soit le triangle ABC de la figure située à gauche. Soit (1,2,3) les 3 angles du triangle ABC. Considérons la droite AC et voyons ce qui se passe autour du point A. Soit la droite (MA) parallèle à (BC). Par les propriértés de conservation des angles par symétrie et par parallélisme, on peut translater les angles 2 et 3 en complément à l'angle 1 autour du point A. C'est ainsi que l'on se rend compte que la somme des 3 angles 1,2,3 forment un angle plat, soit 180 °.

   2. Les 3 médianes d'un triangle se coupent en un point unique, G, centre de gravité de ce triangle. De plus, sur chaque médiane, le point G et située sur cette médiane, au 1/3 du côté opposé par où passe cette médiane et au 2/3 du sommet où passe cette médiane.
      
3. Triangle isocèle
   Propriétés:
   1. La médiane partant du sommet où se coupent les 2 côtés égaux, est confondue avec la hauteur. Conséquence: cette médiane coupe le côté opposé du triangle en formant un angle droit! De même, la hauteur du côté opposé à ce sommet, est égalemnt sa médiatrice.
   2. Les 2 angles formés par l'intersection de chacun des 2 côtés égaux d'un triangle isocèle, avec le 3^ème côté sont égaux.
4. Triangle équilatéral
   Propriétés:
   1. Chaque médiane est confondue avec la hauteur. Conséquence: chaque médiane coupe le côté opposé du triangle en formant un angle droit! De même, la hauteur du côté opposé à ce sommet, est égalemnt sa médiatrice.
      Preuve: c'est une généralisation de la même propriété pour le triangle isocèle.
   2. Chacun des 3 angles a une mesure de 60 °.
      Preuve: les 3 côtés ayant la même longueur, les 3 angles du triangles sont égaux (..à démontrer..). Puisque la somme des 3 angles d'un triangle fait 180 °, on a 3*a=180 ° (a étant la mesure d'ubn de ces angles). Donc chaque angle fait 60 °.

---