Sommaire.
Fiches complète et vérifiée

A propos des angles

1. Angle d'un cercle
   

   Prenons un cercle dont un angle Alpha est défini par la zone rouge sur l'image de gauche. Si cet angle faisait un tour complet, sa mesure serait de : 360 ° 400 gr 2×PI rad Toutes les autres mesure de ce cercle sont des portions de cet angle, à 2×k×PI prêt.

2. Définitions
   • Angle aigu : angle dont la mesure a est comprise entre 0 ° (non inclus) et 90 ° (non inclus).
     0 ° <a<90 °
   • Angle obtus : angle dont la mesure a est comprise entre 90 ° (non inclus) et 180 ° (non inclus).
     90 ° <a<180 °
   • Angle droit : angle dont la mesure a est de 90 °.
   • Angle plat : angle dont la mesure a est de 180 °.
3. Symétrie angulaire
   

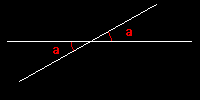
   Soit 2 droites D et D' sécantes. L'angle "a" formé par l'intersection est le même que son symétrique par rapport au point d'intersection des 2 droites. En effet, si on considère les 2 demi-droites partant du point d'intersection et qu'on leur fait faire une rotation de 180 °, on obtient 2 autres demi-droites dont l'angle a est conservé (0+180 ° et a+180 °).

4. Conservation de l'angle par palallélisme
   

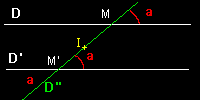
   Soit 2 droites D et D' parallèles. Soit une 3ème droite D'' sécante aux 2 premières. Alors l'angle formé par le croisement de D et D'' a la même mesure que l'angle formé entre D' et D''. En effet, du fait que D' est parallèle à D, l'angle a est conservé (+90° puis -90°) au dessus et en dessous de cette droite.

---