Sommaire.
Fiches complète et vérifiée

Règles de bases de résolutions d'équations

1. Règle de conservation de l'égalité
   1. Addition/Soustraction

      Pour tout nombre x, y, z appartenant à l'ensemble des réels (ou des nombres complexes), si x=y-z, alors x+z=y.

      Démonstration.
      

      Imaginons 2 sacs de graines dont on ne connait pas la quantité. Soit x le nombre de graines du premier sac et y, le nombre de graines du second (on va supposer, pour simplifier, que y est supérieur à x). Si on compte le nombre de graines de chacun des sac, on se rendra compte que "y" contient "z" graines de plus que "x". Ce qui permet aussi de dire que "x" contient "z" graines de moins que "y". On peut également écrire x=y-z équivaut à x+z=y-z+z (en ajoutant la même valeur aux 2 membres de l'égalité, on conserve cette égalité). D'où x=y-z entraîne x+z=y

   2. Multiplication/Division

      Pour tout nombre x, y, z appartenant à l'ensemble des réels (ou des nombres complexes), si x=y/z, alors x.z=y.

      Démonstration.
      

      On peut également écrire x=y/z équivaut à x.z=y/z.z (en multipliant la même valeur aux 2 membres de l'égalité, on conserve cette égalité). D'où x=y/z entraîne x.z=y

2. Distributivité de l'addition par rapport à la multiplication (Niveau collège)

   Pour tous nombres A1, A2 et B1,B2 appartenant à l'ensemble des réels (ou des nombres complexes), alors: (A1+A2).(B1+B2) = A1.B1 + A1.B2 + A2.B1 + A2.B2 Cette règle peut s'appliquer avec n membre dans la première parenthèse et m membres dans la deuxième (niveau lycée ou enseignement supérieur) (A1+<..>+An).(B1+<..>+Bm) = A1.B1 + A1.B2 +<..>+ A1.Bm +<..>+ An.B1 +<..>+An.Bm

   Démonstration.
   

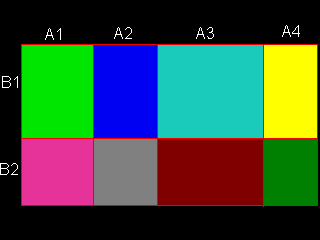
   Cette démonstration est uniquement géométrique. On sait que la surface d'un rectangle est S=L.l (avec "S" = surface du rectangle, "L" = longueur du rectangle et "l" = largeur du rectangle) Ici, la démonstration s'applique sur un rectangle ayant pour longueur (A1+A2+A3+A4) et pour largeur (B1+B2). Mais elle peut s'appliquer avec n'importe quel rectangle morcelé en m.n zones. Nous voyons bien que la surface totale du rectangle de l'image est: S = (A1.B1) + (A2.B1) + (A3.B1) + (A4.B1) + (A1.B2) + (A2.B2) + (A3.B2) + (A4.B2) et... S=(A1+A2+A3+A4).(B1+B2) d'où... (A1+A2+A3+A4) . (B1+B2)= (A1.B1) + (A2.B1) + (A3.B1) + (A4.B1) + (A1.B2) + (A2.B2) + (A3.B2) + (A4.B2) C'est ce qu'il fallait démontrer...

---